dev/script/__Lib/diffcalc-2.1/doc/source/youmanual.rst

Diffcalc User Guide (You Engine)

Diffcalc: A diffraction condition calculator for diffractometer control

Author

Rob Walton

Contact

rob.walton (at) diamond (dot) ac (dot) uk

Website

https://github.com/DiamondLightSource/diffcalc

See also the quickstart guide at github

Introduction

This manual assumes that you are running Diffcalc within OpenGDA or have started it using IPython. It assumes that Diffcalc has been configured for the six circle diffractometer pictured here:

4s + 2d six-circle diffractometer, from H.You (1999)

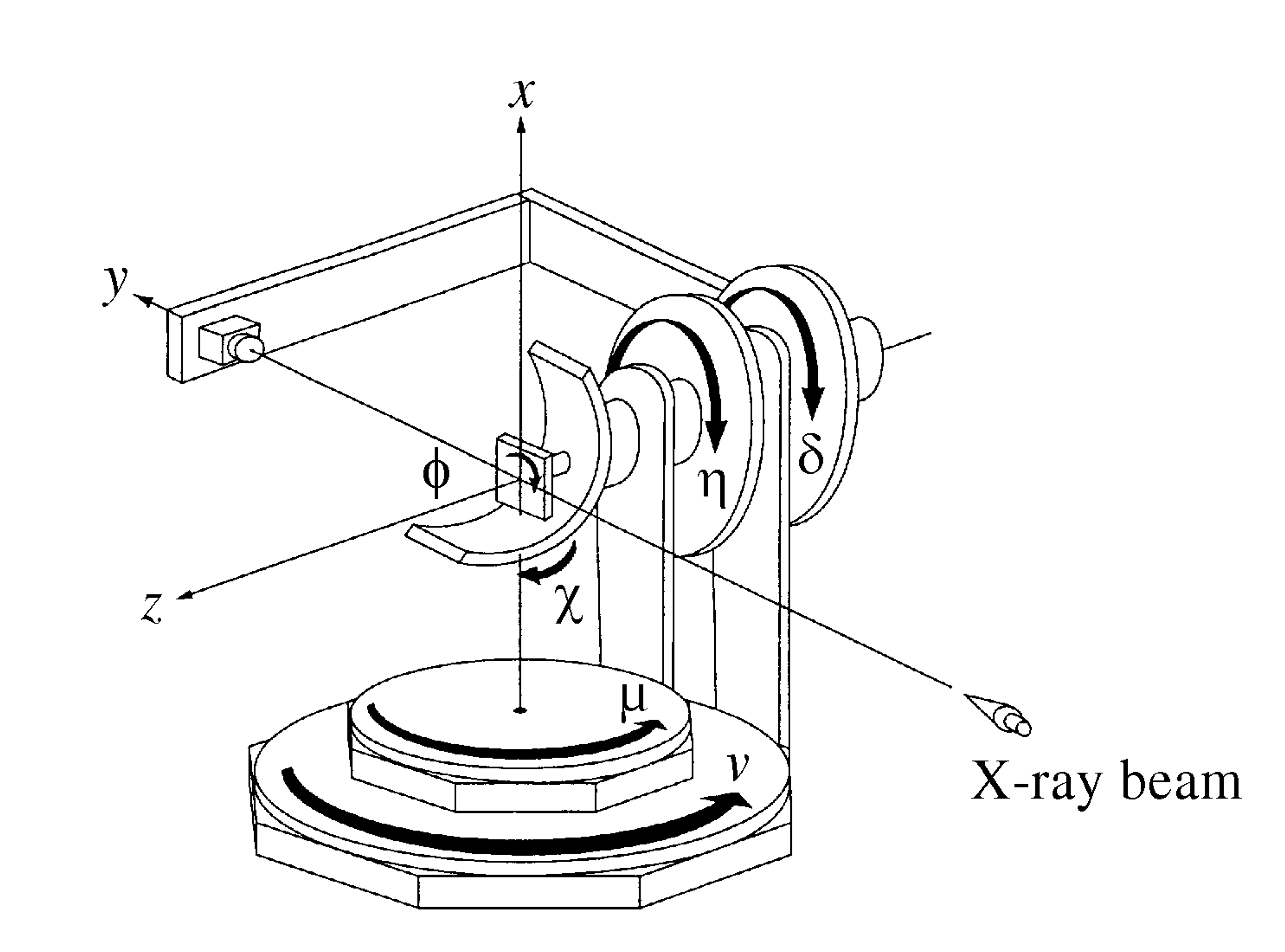
Your Diffcalc configuration may have been customised for the geometry of your diffractometer and possibly the types of experiment you perform. For example, a five-circle diffractometer might be missing the nu circle above.

The laboratory frame is shown above. With all settings at zero as shown the crystal cartesian frame aligns with the laboratory frame. Therefor a cubic crystal mounted squarely in a way that the U matrix (defined below) is unitary will have h||a||x, k||b||y & l||c||z, crystal and reciprocal-lattice coordinate frames are defined with respect to the beam and to gravity to be (for a cubic crystal):

Overview

The following assumes that the diffractometer has been properly leveled, aligned with the beam and zeroed. See the SPEC fourc manual.

Before moving in hkl space you must calculate a UB matrix by specifying the crystal's lattice parameters (which define the B matrix) and finding two reflections (from which the U matrix defining any mismount can be inferred); and, optionally for surface-diffraction experiments, determine how the surface of the crystal is oriented with respect to the phi axis.

Once a UB matrix has been calculated, the diffractometer may be driven in hkl coordinates. A valid diffractometer setting maps easily into a single hkl value. However for a diffractometer with more than three circles there are excess degrees of freedom when calculating a diffractometer setting from an hkl value. Diffcalc provides modes for using up the excess degrees of freedom.

Diffcalc does not perform scans directly. Instead, Scannables that use diffcalc to map between reciprocal lattice space and real diffractometer settings are scanned using the Gda's (or minigda's) generic scan mechanism.

Theory

Thanks to Elias Vlieg for sharing his dos based DIF software that Diffcalc has borrowed heavily from. The version of Diffcalc described here is based on papers by pHH. You. [You1999] and Busing & Levy [Busing1967]. (See also the THANKS.txt file.)

Getting Help

There are few commands to remember. If a command is called without arguments in some cases Diffcalc will prompt for arguments and provide sensible defaults which can be chosen by pressing enter.

Orientation. The helpub command lists all commands related with crystal orientation and the reference vector (often used with surfaces). See the Orientation Commands section at the end of this manual:

>>> help ub
...

HKL movement. The help hkl list all commands related to moving in reciprocal-lattice space. See the Motion Commands section at the end of this manual:

>>> help hkl
...

Call help on any command. e.g.:

>>> help loadub
loadub (diffcalc command):
loadub 'name' | num -- load an existing ub calculation

Diffcalc's Scannables

To list and show the current positions of your beamline's scannables use pos with no arguments:

>>> pos

Results in:

Energy and wavelength scannables:

energy    12.3984
wl:       1.0000

Diffractometer scannables, as a group and in component axes (in the real GDA these have limits):

sixc:     mu: 0.0000 delta: 0.0000 gamma: 0.0000 omega: 0.0000 chi: 0.0000 phi: 0.0000
mu:       0.0000
chi:      0.0000
delta:    0.0000
gamma:    0.0000
omega:    0.0000
phi:      0.0000

Dummy counter, which in this example simply counts at 1hit/s:

ct:      0.0000

Hkl scannable, as a group and in component:

hkl:      Error: No UB matrix
h:        Error: No UB matrix
k:        Error: No UB matrix
l:        Error: No UB matrix

Parameter scannables, used in some modes, these provide a scannable alternative to the Motion section. Some constrain of these constrain virtual angles:

alpha:    ---
beta:     ---
naz:      ---
psi:      ---
qaz:      ---

and some constrain physical angles:

phi_con:  ---
chi_con:  ---
delta_con:---
eta_con:  ---
gam_con:  ---
mu_con:   ---

Crystal orientation

Before moving in hkl space you must calculate a UB matrix by specifying the crystal's lattice parameters (which define the B matrix) and finding two reflections (from which the U matrix can be inferred); and, optionally for surface-diffraction experiments, determine how the surface of the crystal is oriented with respect to the phi axis.

Start a new UB calculation

A UB calculation contains the description of the crystal-under-test, any saved reflections, reference angle direction, and a B & UB matrix pair if they have been calculated or manually specified. Starting a new UB calculation will clear all of these.

Before starting a UB-calculation, the ub command used to summarise the state of the current UB-calculation, will reflect that no UB-calculation has been started:

>>> ub
<<< No UB calculation started >>>

A new UB-calculation calculation may be started and lattice specified explicitly:

>>> newub 'example'
>>> setlat '1Acube' 1 1 1 90 90 90

or interactively:

>>> newub
calculation name: example
crystal name: 1Acube
       a [1]: 1
       b [1]: 1
       c [1]: 1
  alpha [90]: 90
   beta [90]: 90
  gamma [90]: 90

where a,b and c are the lengths of the three unit cell basis vectors in Angstroms, and alpha, beta and gamma are angles in Degrees.

The ub command will show the state of the current UB-calculation (and the current energy for reference):

>>> ub
UBCALC

   name:       example

   n_phi:      0.00000   0.00000   1.00000 <- set

CRYSTAL

   name:        1Acube

   a, b, c:    1.00000   1.00000   1.00000
              90.00000  90.00000  90.00000

   B matrix:   6.28319   0.00000   0.00000
               0.00000   6.28319   0.00000
               0.00000   0.00000   6.28319

UB MATRIX

   <<< none calculated >>>

REFLECTIONS

   <<< none specified >>>

CRYSTAL ORIENTATIONS

<<< none specified >>>

Load a UB calculation

To load the last used UB-calculation:

>>> lastub
Loading ub calculation: 'mono-Si'

To load a previous UB-calculation:

>>> listub
UB calculations in: /Users/walton/.diffcalc/i16

0) mono-Si            15 Feb 2017 (22:32)
1) i16-32             13 Feb 2017 (18:32)

>>> loadub 0

Generate a U matrix from two reflections

The normal way to calculate a U matrix is to find the position of two reflections with known hkl values. Diffcalc allows many reflections to be recorded but currently only uses the first two when calculating a UB matrix.

Find U matrix from two reflections:

>>> pos wl 1
wl:        1.0000
>>> c2th [0 0 1]
59.99999999999999

>>> pos sixc [0 60 0 30 90 0]
sixc:     mu:  0.0000 delta:  60.0000 gam:  0.0000 eta:  30.0000 chi:  90.0000 phi:  0.0000 
>>> addref [0 0 1]

>>> pos sixc [0 90 0 45 45 90]
sixc:     mu:  0.0000 delta:  90.0000 gam:  0.0000 eta:  45.0000 chi:  45.0000 phi:  90.0000 
>>> addref [0 1 1]
Calculating UB matrix.

Check that it looks good:

>>> checkub

     ENERGY     H     K     L    H_COMP   K_COMP   L_COMP     TAG
 1  12.3984  0.00  0.00  1.00    0.0000   0.0000   1.0000        
 2  12.3984  0.00  1.00  1.00    0.0000   1.0000   1.0000        

Generate a U matrix from one reflection

To estimate based on first reflection only:

>>> trialub
resulting U angle: 0.00000 deg
resulting U axis direction: [-1.00000,  0.00000,  0.00000]
Recalculating UB matrix from the first reflection only.
NOTE: A new UB matrix will not be automatically calculated when the orientation reflections are modified.

Edit reflection list

Use showref to show the reflection list:

>>> showref
     ENERGY     H     K     L        MU    DELTA      GAM      ETA      CHI      PHI  TAG
   1 12.398  0.00  0.00  1.00    0.0000  60.0000   0.0000  30.0000  90.0000   0.0000  
   2 12.398  0.00  1.00  1.00    0.0000  90.0000   0.0000  45.0000  45.0000  90.0000  

Use swapref to swap reflections:

>>> swapref 1 2
Not calculating UB matrix as it has been manually set. Use 'calcub' to explicitly recalculate it.
Recalculating UB matrix.

Use delref to delete a reflection:

>>> delref 1

Generate a U matrix from two lattice directions

Another approach to calculate a U matrix is to provide orientation of two crystal lattice directions in laboratory frame of reference using addorient command. The first lattice direction will be aligned along the specified in the laboratory frame. The second lattice direction will be used to set azimuthal orientation of the crystal in the plane perpendicular to the first lattice orientation. Diffcalc allows many lattice directions to be recorded but currently uses only the first two when calculating a UB matrix.

Find U matrix from two lattice directions:

>>> addorient [0 0 1] [0 0 1]

>>> addorient [1 0 0] [1 1 0]
Calculating UB matrix.

Calculate a UB matrix

Unless a U or UB matrix has been manually specified, a new UB matrix will be calculated after the second reflection has been found, or whenever one of the first two reflections is changed.

Use the command calcub to force the UB matrix to be calculated from the first two reflections. In case of using lattice orientations instead of reflections, use command orientub to force the UB matrix to be calculated from the first two orientations.

If you have misidentified a reflection used for the orientation the resulting UB matrix will be incorrect. Always use the checkubcommand to check that the computed reflection indices agree with the estimated values:

>>> checkub

     ENERGY     H     K     L    H_COMP   K_COMP   L_COMP     TAG
 1  12.3984  0.00  1.00  1.00    0.0000   1.0000   1.0000        
 2  12.3984  0.00  0.00  1.00    0.0000   0.0000   1.0000        

Calculate a U matrix from crystal mismount

U matrix can be defined from crystal mismount by using a rotation matrix calculated from a provided mismount angle and axis. setmiscut command defines new U matrix by setting it to a rotation matrix calculated from the specified angle and axis parameters. addmiscut command applies the calculated rotation matrix to the existing U matrix, i.e. adds extra mismount to the already existing one:

>>> setmiscut 5 [1 0 0]
n_phi: -0.00000  -0.08716   0.99619
n_hkl:  0.00000   0.00000   1.00000 <- set
normal:
   angle:  5.00000
   axis:  1.00000  -0.00000   0.00000

Manually specify U matrix

Set U matrix manually (pretending sample is squarely mounted):

>>> setu [[1 0 0] [0 1 0] [0 0 1]]
Recalculating UB matrix.
NOTE: A new UB matrix will not be automatically calculated when the orientation reflections are modified.

Refining UB matrix from reflection

UB matrix elements can be refined to match diffractometer settings and crystal orientation experimentally found for a given reflection with the corresponding reflection indices. refineub command rescales crystal unit cell dimensions to match with the found scattering angle value and recalculates mismount parameters to update U matrix:

>>> refineub [1 0 0]
current pos[y]: y
Unit cell scaling factor:  0.99699
Refined crystal lattice:
   a, b, c:  0.99699   0.99699   0.99699
             90.00000  90.00000  90.00000

Update crystal settings?[y]: y
Warning: the old UB calculation has been cleared.
         Use 'calcub' to recalculate with old reflections or
         'orientub' to recalculate with old orientations.
Miscut parameters:
      angle:  2.90000
       axis: -0.00000   1.00000  -0.00000
Apply miscut parameters?[y]: y
   n_phi:  0.67043  -0.00000   0.74198
   n_hkl:  0.00000   0.00000   1.00000 <- set
   normal:
      angle: 42.10000
      axis:  0.00000   1.00000   0.00000

Set the reference vector

When performing surface experiments the reference vector should be set normal to the surface. It can also be used to define other directions within the crystal with which we want to orient the incident or diffracted beam.

By default the reference vector is set parallel to the phi axis. That is, along the z-axis of the phi coordinate frame.

The ub command shows the current reference vector along with the orientation relative to the z-axis, at the top its report (or it can be shown by calling setnphi or setnhkl' with no args):

>>> ub
...
n_phi:      0.00000   0.00000   1.00000 <- set
n_hkl:     -0.00000   0.00000   1.00000
normal:     None
...

The <- set label here indicates that the reference vector is set in the phi coordinate frame. In this case, therefore, its direction in the crystal's reciprocal lattice space is inferred from the UB matrix.

To set the reference vector in the phi coordinate frame use:

>>> setnphi [0 0 1]
...

This is useful if the surface normal has be found with a laser or by x-ray occlusion. This vector must currently be manually calculated from the sample angle settings required to level the surface (sigma and tau commands on the way).

To set the reference vector in the crystal's reciprocal lattice space use (this is a quick way to determine the surface orientation if the surface is known to be cleaved cleanly along a known axis):

>>> setnhkl [0 0 1]
...

Motion

Once a UB matrix has been calculated, the diffractometer may be driven in hkl coordinates. A given diffractometer setting maps easily into a single hkl value. However for a diffractometer with more than three circles there are excess degrees of freedom when calculating a diffractometer setting from an hkl value. Diffcalc provides many for using up the excess degrees of freedom.

By default Diffcalc selects no mode.

Constraining solutions for moving in hkl space

To get help and see current constraints:

>>> help con
...

>>> con
    DET        REF        SAMP
    ------     ------     ------
    delta      a_eq_b     mu
    gam        alpha      eta
    qaz        beta       chi
    naz        psi        phi
                          mu_is_gam

!   3 more constraints required

    Type 'help con' for instructions

Three constraints can be given: zero or one from the DET and REF columns and the remainder from the SAMP column. Not all combinations are currently available. Use help con to see a summary if you run into troubles.

To configure four-circle vertical scattering:

>>> con gam 0 mu 0 a_eq_b
    gam  : 0.0000
    a_eq_b
    mu   : 0.0000

In the following the scattering plane is defined as the plane including the scattering vector, or momentum transfer vector, and the incident beam.

DETECTOR COLUMN:

• delta - physical delta setting (vertical detector motion) del=0 is equivalent to qaz=0
• gam - physical gamma setting (horizontal detector motion) gam=0 is equivalent to qaz=90
• qaz - azimuthal rotation of scattering vector (about the beam, from horizontal)
• naz - azimuthal rotation of reference vector (about the beam, from horizontal)

REFERENCE COLUMN:

• alpha - incident angle to surface (if reference is normal to surface)
• beta - exit angle from surface (if reference is normal to surface)
• psi - azimuthal rotation about scattering vector of reference vector (from scattering plane)
• a_eq_b - bisecting mode with alpha=beta. Equivalent to psi=90

SAMPLE COLUMN:

• mu, eta, chi & phi - physical settings
• mu_is_gam - force mu to follow gamma (results in a 5-circle geometry)

Diffcalc will report two other (un-constrainable) virtual angles:

• theta - half of 2theta, the angle through the diffracted beam bends
• tau - longitude of reference vector from scattering vector (in scattering plane)

Example constraint modes

There is sometimes more than one way to get the same effect.

Vertical four-circle mode:

>>> con gam 0 mu 0 a_eq_b   # or equivalently:
>>> con qaz 90 mu 0 a_eq_b

>>> con alpha 1             # replaces a_eq_b

Horizontal four-circle mode:

>>> con del 0 eta 0 alpha 1   # or equivalently:
>>> con qaz 0 mu 0 alpha 1

Surface vertical mode:

>>> con naz 90 mu 0 alpha 1

Surface horizontal mode:

>>> con naz 0 eta 0 alpha 1

Z-axis mode (surface horizontal):

>>> con chi (-sigma) phi (-tau) alpha 1

where sigma and tau are the offsets required in chi and phi to bring the surface normal parallel to eta. Alpha will determine mu directly leaving eta to orient the planes. Or:

>>> con naz 0 phi 0 alpha 1  # or any another sample angle

Z-axis mode (surface vertical):

>>> con naz 0 phi 0 alpha 1  # or any another sample angle

Changing constrained values

Once constraints are chosen constrained values may be changed directly:

>>> con mu 10
    gam  : 0.0000
    a_eq_b
    mu   : 10.0000

or via the associated scannable:

>>> pos mu_con 10
mu_con:   10.00000

Configuring limits and cuts

Diffcalc maintains its own limits on axes. These limits will be used when choosing solutions. If more than one detector solution is exists Diffcalc will ask you to reduce the the limits until there is only one. However if more than one solution for the sample settings is available it will choose one base on heuristics.

Use the hardware command to see the current limits and cuts:

>>> hardware
               mu           (cut: -180.0)
            delta           (cut: -180.0)
              gam           (cut: -180.0)
              eta           (cut: -180.0)
              chi           (cut: -180.0)
              phi           (cut:    0.0)
Note: When auto sector/transforms are used,
       cuts are applied before checking limits.

To set the limits:

>>> setmin delta -1
>>> setmax delta 145

To set a cut:

>>> setcut phi -180

This causes requests to move phi to be between the configured -180 and +360 degress above this. i.e. it might dive to -10 degrees rather than 350.

Moving in hkl space

Configure a mode, e.g. four-circle vertical:

>>> con gam 0 mu 0 a_eq_b
    gam  : 0.0000
    a_eq_b
    mu   : 0.0000

Simulate moving to a reflection:

>>> sim hkl [0 1 1]
sixc would move to:
     mu :    0.0000
  delta :   90.0000
    gam :    0.0000
    eta :   45.0000
    chi :   45.0000
    phi :   90.0000

  alpha :   30.0000
   beta :   30.0000
    naz :   35.2644
    psi :   90.0000
    qaz :   90.0000
    tau :   45.0000
  theta :   45.0000

Move to reflection:

>>> pos hkl [0 1 1]
hkl:      h: 0.00000 k: 1.00000 l: 1.00000 

>>> pos sixc
sixc:     mu:  0.0000 delta:  90.0000 gam:  0.0000 eta:  45.0000 chi:  45.0000 phi:  90.0000 

Simulate moving to a location:

>>> pos sixc [0 60 0 30 90 0]
sixc:     mu:  0.0000 delta:  60.0000 gam:  0.0000 eta:  30.0000 chi:  90.0000 phi:  0.0000 

Scanning in hkl space

All scans described below use the same generic scanning mechanism provided by the GDA system or by minigda. Here are some examples.

Fixed hkl scans

In a 'fixed hkl scan' something (such as energy or Bin) is scanned, and at each step hkl is 'moved' to keep the sample and detector aligned. Also plonk the diffractometer scannable (sixc) on there with no destination to monitor what is actually happening and then throw on a detector (ct) with an exposure time if appropriate:

>>> #scan scannable_name start stop step [scannable_name [pos or time]]..

>>> scan en 9 11 .5 hkl [1 0 0] sixc ct 1

>>> scan en 9 11 .5 hklverbose [1 0 0] sixc ct 1

>>> scan betain 4 5 .2 hkl [1 0 0] sixc ct 1

>>> scan alpha_par 0 10 2 hkl [1 0 0] sixc ct 1

Scanning hkl

Hkl, or one component, may also be scanned directly:

>>> scan h .8 1.2 .1 hklverbose sixc ct 1

At each step, this will read the current hkl position, modify the h component and then move to the resulting vector. There is a danger that with this method k and l may drift. To get around this the start, stop and step values may also be specified as vectors. So for example:

>>> scan hkl [1 0 0] [1 .3 0] [1 0.1 0] ct1

is equivilant to:

>>> pos hkl [1 0 0]
>>> scan k 0 .3 .1 ct1

but will not suffer from drifting. This method also allows scans along any direction in hkl space to be performed.

Multidimension scans

Two and three dimensional scans:

>>> scan en 9 11 .5 h .9 1.1 .2 hklverbose sixc ct 1
>>> scan h 1 3 1 k 1 3 1 l 1 3 1 hkl ct 1

Commands

Orientation Commands

STATE
-- newub {'name'}	start a new ub calculation name
-- loadub 'name' | num	load an existing ub calculation
-- lastub	load the last used ub calculation
-- listub	list the ub calculations available to load
-- rmub 'name'|num	remove existing ub calculation
-- saveubas 'name'	save the ub calculation with a new name
LATTICE
-- setlat	interactively enter lattice parameters (Angstroms and Deg)
-- setlat name a	assumes cubic
-- setlat name a b	assumes tetragonal
-- setlat name a b c	assumes ortho
-- setlat name a b c gamma	assumes mon/hex with gam not equal to 90
-- setlat name a b c alpha beta gamma	arbitrary
-- c2th [h k l]	calculate two-theta angle for reflection
-- hklangle [h1 k1 l1] [h2 k2 l2]	calculate angle between [h1 k1 l1] and [h2 k2 l2] crystal planes
REFERENCE (SURFACE)
-- setnphi {[x y z]}	sets or displays n_phi reference
-- setnhkl {[h k l]}	sets or displays n_hkl reference
REFLECTIONS
-- showref	shows full reflection list
-- addref	add reflection interactively
-- addref [h k l] {'tag'}	add reflection with current position and energy
-- addref [h k l] (p1, .., pN) energy {'tag'}	add arbitrary reflection
-- editref num	interactively edit a reflection
-- delref num	deletes a reflection (numbered from 1)
-- clearref	deletes all the reflections
-- swapref	swaps first two reflections used for calculating U matrix
-- swapref num1 num2	swaps two reflections (numbered from 1)
CRYSTAL ORIENTATIONS
-- showorient	shows full list of crystal orientations
-- addorient	add crystal orientation interactively
-- addorient [h k l] [x y z] {'tag'}	add crystal orientation in laboratory frame
-- editorient num	interactively edit a crystal orientation
-- delorient num	deletes a crystal orientation (numbered from 1)
-- clearorient	deletes all the crystal orientations
-- swaporient	swaps first two crystal orientations used for calculating U matrix
-- swaporient num1 num2	swaps two crystal orientations (numbered from 1)
UB MATRIX
-- checkub	show calculated and entered hkl values for reflections
-- setu {..][..][..}	manually set u matrix
-- setub {..][..][..}	manually set ub matrix
-- calcub	(re)calculate u matrix from ref1 and ref2
-- trialub	(re)calculate u matrix from ref1 only (check carefully)
-- refineub {[h k l]} {pos}	refine unit cell dimensions and U matrix to match diffractometer angles for a given hkl value
-- addmiscut angle {[x y z]}	apply miscut to U matrix using a specified miscut angle in degrees and a rotation axis (default: [0 1 0])
-- setmiscut angle {[x y z]}	manually set U matrix using a specified miscut angle in degrees and a rotation axis (default: [0 1 0])

Motion commands

CONSTRAINTS
-- con	list available constraints and values
-- con <name> {val}	constrains and optionally sets one constraint
-- con <name> {val} <name> {val} <name> {val}	clears and then fully constrains
-- uncon <name>	remove constraint
HKL
-- allhkl [h k l]	print all hkl solutions ignoring limits
HARDWARE
-- hardware	show diffcalc limits and cuts
-- setcut {name {val}}	sets cut angle
-- setmin {axis {val}}	set lower limits used by auto sector code (None to clear)
-- setmax {name {val}}	sets upper limits used by auto sector code (None to clear)
MOTION
-- sim hkl scn	simulates moving scannable (not all)
-- sixc	show Eularian position
-- pos sixc [mu, delta, gam, eta, chi, phi]	move to Eularian position(None holds an axis still)
-- sim sixc [mu, delta, gam, eta, chi, phi]	simulate move to Eulerian positionsixc
-- hkl	show hkl position
-- pos hkl [h k l]	move to hkl position
-- pos {h | k | l} val	move h, k or l to val
-- sim hkl [h k l]	simulate move to hkl position

Good luck --- RobW

References

Busing1967

W. R. Busing and H. A. Levy. Angle calculations for 3- and 4-circle X-ray and neutron diffractometers. Acta Cryst. (1967). 22, 457-464. (pdf link).

You1999

8. You. Angle calculations for a '4S+2D' six-circle diffractometer.

J. Appl. Cryst. (1999). 32, 614-623. (pdf link).