dev/script/__Lib/diffcalc/README_template.rst

Diffcalc - A Diffraction Condition Calculator for Diffractometer Control

Diffcalc is a python/jython based diffraction condition calculator used for controlling diffractometers within reciprocal lattice space. It performs the same task as the fourc, sixc, twoc, kappa, psic and surf macros from SPEC.

There is a user guide and developer guide, both at diffcalc.readthedocs.io

Software compatibility

• Written in Python using numpy
• Works in Jython using Jama
• Runs directly in OpenGDA<http://www.opengda.org>
• Runs in in Python or IPython using minimal OpenGda emulation (included)
• Contact us for help running in your environment

Diffractometer compatibility

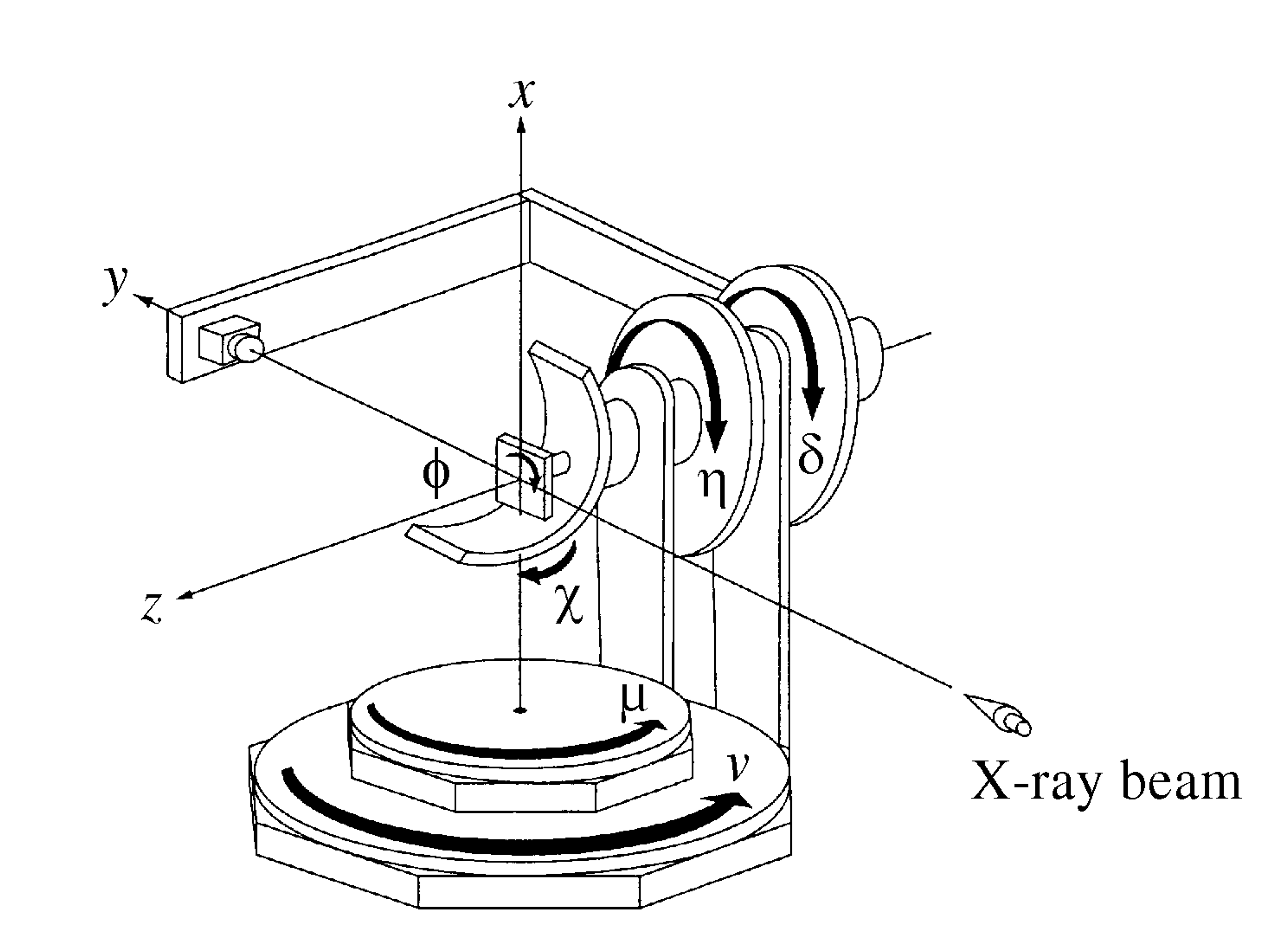
Diffcalc’s standard calculation engine is an implementation of [You1999] and [Busing1967]. Diffcalc works with any diffractometer which is a subset of:

Diffcalc can be configured to work with any diffractometer geometry which is a subset of this. For example, a five-circle diffractometer might be missing the nu circle above.

Note that the first versions of Diffcalc were based on [Vlieg1993] and [Vlieg1998] and a ‘Vlieg’ engine is still available. There is also an engine based on [Willmott2011]. The ‘You’ engine is more generic and the plan is to remove the old ‘Vlieg’ engine once beamlines have been migrated.

If we choose the x axis parallel to b, the yaxis intheplaneofblandb2,andthezaxis perpendicular to that plane,

Installation

Check it out:

$ git clone https://github.com/DiamondLightSource/diffcalc.git
Cloning into 'diffcalc'...

At Diamond Diffcalc may be installed within an OpenGDA deployment and is available via the 'module' system from bash.

Starting

Start diffcalc in ipython using a sixcircle dummy diffractometer:

$ cd diffcalc
$ ./diffcalc.py --help
...

$ ./diffcalc.py sixcircle

Running: "ipython --no-banner --HistoryManager.hist_file=/tmp/ipython_hist_zrb13439.sqlite -i -m diffcmd.start sixcircle False"

---------------------------------- DIFFCALC -----------------------------------
Startup script: '/Users/zrb13439/git/diffcalc/startup/sixcircle.py'
Loading ub calculation: 'test'
------------------------------------ Help -------------------------------------
Quick:  https://github.com/DiamondLightSource/diffcalc/blob/master/README.rst
Manual: https://diffcalc.readthedocs.io
Type:   > help ub
        > help hkl
-------------------------------------------------------------------------------
In [1]:

Within Diamond use:

$ module load diffcalc
$ diffcalc --help
...
$ diffcalc sixcircle

Trying it out

Type demo.all() to see it working and then move try the following quick start guide:

>>> demo.all()
...

Getting help

To view help with orientation and then moving in hkl space:

>>> help ub
...
>>> help hkl
...

Configuring a UB calculation

See the full user manual<https://diffcalc.readthedocs.io> for many more options and an explanation of what this all means.

To load the last used UB-calculation:

>>> lastub
Loading ub calculation: 'mono-Si'

To load a previous UB-calculation:

>>> listub
UB calculations in: /Users/walton/.diffcalc/i16

0) mono-Si            15 Feb 2017 (22:32)
1) i16-32             13 Feb 2017 (18:32)

>>> loadub 0

To create a new UB-calculation:

==> newub 'example'
==> setlat '1Acube' 1 1 1 90 90 90

where the basis is defined by Busing & Levy:

"...we choose the x axis parallel to b, the y axis in the plane of bl and b2, and the zaxis perpendicular to that plane."

Find U matrix from two reflections:

==> pos wl 1
==> c2th [0 0 1]
59.99999999999999

==> pos sixc [0 60 0 30 90 0]
==> addref [0 0 1]

==> pos sixc [0 90 0 45 45 90]
==> addref [0 1 1]

Check that it looks good:

==> checkub

To see the resulting UB-calculation:

==> ub

Setting the reference vector

See the full user manual<https://diffcalc.readthedocs.io> for many more options and an explanation of what this all means.

By default the reference vector is set parallel to the phi axis. That is, along the z-axis of the phi coordinate frame.

The ub command shows the current reference vector, along with any inferred miscut, at the top its report (or it can be shown by calling setnphi or setnhkl' with no args):

>>> ub
...
n_phi:      0.00000   0.00000   1.00000 <- set
n_hkl:     -0.00000   0.00000   1.00000
miscut:     None
...

Constraining solutions for moving in hkl space

See the full user manual<https://diffcalc.readthedocs.io> for many more options and an explanation of what this all means.

To get help and see current constraints:

>>> help con
...

==> con

Three constraints can be given: zero or one from the DET and REF columns and the remainder from the SAMP column. Not all combinations are currently available. Use help con to see a summary if you run into troubles.

To configure four-circle vertical scattering:

==> con gam 0 mu 0 a_eq_b

Moving in hkl space

Simulate moving to a reflection:

==> sim hkl [0 1 1]

Move to reflection:

==> pos hkl [0 1 1]

==> pos sixc

Scanning in hkl space

Scan an hkl axis (and read back settings):

==> scan l 0 1 .2 sixc

Scan a constraint (and read back virtual angles and eta):

==> con psi
==> scan psi 70 110 10 hklverbose [0 1 1] eta

Orientation Commands

==> UB_HELP_TABLE

Motion Commands

==> HKL_HELP_TABLE

References

Busing1967

W. R. Busing and H. A. Levy. Angle calculations for 3- and 4-circle X-ray and neutron diffractometers. Acta Cryst. (1967). 22, 457-464. (pdf link).

Vlieg1993

Martin Lohmeier and Elias Vlieg. Angle calculations for a six-circle surface x-ray diffractometer. J. Appl. Cryst. (1993). 26, 706-716. (pdf link).

Vlieg1998

Elias Vlieg. A (2+3)-type surface diffractometer: mergence of the z-axis and (2+2)-type geometries. J. Appl. Cryst. (1998). 31, 198-203. (pdf link).

Willmott2011

3. 13. Schlepütz, S. O. Mariager, S. A. Pauli, R. Feidenhans'l and

P. R. Willmott. Angle calculations for a (2+3)-type diffractometer: focus on area detectors. J. Appl. Cryst. (2011). 44, 73-83. (pdf link).

You1999

8. You. Angle calculations for a '4S+2D' six-circle diffractometer.

J. Appl. Cryst. (1999). 32, 614-623. (pdf link).